- About Us
About RSIS International
Publication Method
Conference
Contact Us
- Journals
- Conference Proceedings
Days
Hours
Minutes
Seconds
Submission Deadline
IMPACT OF CCRI ON LEARNERS’ ACHIEVEMENT IN PRIMARY SCHOOL MATHEMATICS, A CASE STUDY OF BOMET EAST SUB-COUNTY, KENYA
1Dr. John K. Keter, 2Dr. Joseph K. Bii and 3Dr. Beatrice C. Chepkwony
1,2 & 3Department of Curriculum, Instruction and Educational Media (CIEM) University of Kabianga School of Education, Arts and Social Sciences
Cooperative Constructivist Remedial Instruction (CCRI) is an emerging pedagogy among the teaching community across the world especially in the 21st century. However, its effect on learners’ achievement remains unknown. This innovative approach to teaching takes cognizance of both social and cognitive constructivism. Constructivism emphasizes on how the learner constructs knowledge from the experiences provided, which is unique to each individual learner. The approach gives learners the opportunity to construct knowledge in collaboration with their peers. Such an opportunity encourages them to progress to higher levels of academic achievement. Solomon’s Four Non-equivalent Control Group Design incorporating quantitative techniques was used in the study. The CCRI approach to teaching through the 5E’s learning (Engage-Explore-Explain-Elaborate-Evaluate) model was applied to Experimental Groups while the Conventional Teaching Methods (CTM) were used to teach the Control Groups where total of 211 Standard eight pupils from four randomly selected schools participated in the study. A Mathematics Achievement Test (MAT) was administered as a pre-test to estimate the learner’s achievement before intervention. The intervention period lasted for five weeks. Thereafter, items in the MAT were rearranged and administered to all the four groups as a post-test to measure the impact of CCRI relative to CTM on pupils’ achievement in Mathematics. The results from the study revealed that CCRI approach significantly improved learners’ achievement in Mathematics compared to the use of CTM. Secondly CCRI approach was equally effective in improving achievement of both boys and girls in Mathematics. Their improved level of achievement in the subject is attributed to their enhanced motivation as a result of increased teacher-leaner and learner-learner interaction during lessons as advocated by CCRI approach.
Key Words: Cooperative Constructivist Remedial Instruction, 5E’s Model, Learners’ Academic Achievement, Primary School Mathematics
Unlike many academic subjects, Mathematics learning builds upon itself level by level. Therefore, it is important to start with a strong foundation especially in Primary School level of learning. Bharadwaj (2010) points out that Mathematics is an essential support of mankind civilization. The society in general takes the subject as the foundation of Scientific and Technological knowledge that is crucial in social-economic development of every nation. According to Allosopp, Kyger and Lovin (2007), pupils without appropriate level of competency in Mathematics will find it difficult to manage many important aspects of their lives and also limit their career opportunities in future. However, the falling standards of learners’ achievement in Mathematics have triggered a lot of concern among researchers, educationists, parents and other stakeholders to find an appropriate solution to this perennial poor performance in the subject in Kenya.
In the year 2020, a total of 1,180,337 candidates sat for the KCPE Mathematics examination nationally. Table 1 shows National performance in KCPE Mathematics examination from 2016-2020.
Table 1: National performance in KCPE Mathematics
| Year | 2020 | 2019 | 2018 | 2017 | 2016 |
| National % Mean Score | 27.45 | 24.65 | 21.57 | 25.57 | 22.70 |
| Standard Deviation | 11.21 | 11.03 | 8.57 | 10.41 | 9.35 |
Source: KNEC Report 2021
From the results in Table 1 it can be observed that the overall performance in year 2020 KCPE Mathematics improved significantly compared to the performance in the year 2019, both in mean and standard deviation. The improvement noted in performance can be attributed to the mastery of content by the candidates which enabled them to perform fairly well in the examined paper (KNEC, 2020). However, the percentage mean has been below average over the years.
In Kenyan education, while there’s no universal consensus on a significant gender gap in Mathematics performance the subject has been gender-marked with males seen to be doing better than girls (McCoy et al., 2022). This perception of gender differences is severally reflected in the student’s actual Mathematics performance. Table 2 shows the general performance in 2020 KCPE Mathematics by gender compared to the last two years.
Table 2: General Performance in 2018-2020 KCPE Mathematics by Gender compared to the last two years
| Year | 2020 | 2019 | 2018 | |||
| Gender | Male | Female | Male | Female | Male | Female |
| Entry | 591,151 | 589,186 | 542,614 | 538,897 | 527,245 | 524,942 |
| National Raw % Mean | 27.94 | 26.97 | 25.42 | 23.87 | 22.06 | 27.38 |
| Standard Deviation | 11.55 | 10.84 | 11.40 | 10.59 | 8.94 | 8.05 |
The data in Table 2 shows that the candidature of both boys and girls has continued to increase over the three years. In the year 2020, male candidates performed better with a mean score of 27.94 compared to Female candidates who had a mean of 26.97. Moreover, Male candidates had a better spread in scores distribution with a standard deviation of 11.55 compared to female candidates who registered a standard deviation of 10.84. There were slightly more male candidates than female who sat for the Mathematics paper. Although the performance in the subject is below average, both male and female candidates performed well compared to the previous year 2019. Bomet County is no exception. The performance in KCPE Mathematics has remained low over the years. Table 3 shows an analysis of Mathematics KCPE results for each of the sub-counties for the period 2016-2020.
Table 3: Bomet County performance in KCPE Mathematics per Sub-county
| Sub-County | 2020 | 2019 | 2018 | 2017 | 2016 | Overall Mean |
| Bomet East | 26.67 | 28.33 | 29.17 | 25.00 | 28.33 | 27.50 |
| Bomet Central | 30.00 | 31.67 | 34.17 | 34.17 | 36.67 | 33.33 |
| Chepalungu | 32.50 | 30.00 | 35.83 | 39.17 | 37.50 | 33.33 |
| Konoin | 33.33 | 35.00 | 33.33 | 38.33 | 39.17 | 35.83 |
| Sotik | 30.00 | 29.17 | 26.67 | 30.00 | 32.50 | 30.00 |
| Total | 30.83 | 30.88 | 31.86 | 32.50 | 35.24 |
The performance in KCPE Mathematics has remained low over the years. Results in Table 3 indicates that the performance has been below average over the years. Furthermore, the performance in Bomet East sub-county has been the least compared to the other 5 sub-counties. This justifies the selection of Bomet East for the purpose of this study. Moreover, gender disparity in Mathematics achievement is quite pronounced in the Sub-county. Table 4 shows the performance in the subject by gender.
Table 4: Performance by Gender in KCPE Mathematics in Bomet East Sub-county
| Year | 2020 | 2019 | 2018 | |||
| Gender | Male | Female | Male | Female | Male | Female |
| Entry | 11,332 | 10,234 | 10,500 | 9,800 | 10,112 | 9,289 |
| National % Mean | 28.58 | 24.76 | 29.88 | 26.78 | 29.98 | 28.46 |
| Standard Deviation | 7.88 | 8.65 | 9.66 | 10.79 | 9.83 | 9.77 |
Results in Table 4 indicates that the candidature of both male and female has continued to grow over the years. Generally, the performance in the sub-county in Mathematics has been below average across the years. Boys have continued to outshine their female counterparts in the subject.
Currently, instruction in most basic schools is non-interactive, and this encourages pupils to learn by rote memorization (Gyasi, 2003). Teachers usually struggle between their desire to cover a lot of content and the necessity of using more time-consuming methods that allow pupils to construct meaning from their lessons (Franklin, 2001). This notion is a general haste to cover topics without necessarily giving pupils the opportunity to acquire deeper understanding of the topics (Anamuah-Mensah, Mereku & Ghartey-Ampiah, 2008). Teaching kids robust Mathematics skills through constructivism supports their future love of learning and avoiding anxiety, phobia and stigma in the subject.
Recent research in education reforms has revealed a move from teacher-centred and didactic learning environments to an adoption of student-centred constructivist methods (Kolb & Kolb, 2005; Lee, 2007). Constructivist view of learning emphasizes the significance of the individual learner’s prior knowledge in helping the learner to learn (Wu & Tsai, 2005). Currently, emphasis is placed on learning as a ‘process’ rather than an objectivist view which concentrates on ‘outcome’ (Killen, 2007). The constructivist revolution offers an active sense-maker and suggests new innovative methods of instruction such as Cooperative Constructivism Remedial Instruction (CCRI) that could help in motivating learners with difficulties in Mathematics consequently enhancing their academic achievement in the subject. CCRI approach to teaching through the 5E’s learning (Engage-Explore-Explain-Elaborate-Evaluate) strategy facilitates presentations of materials in a constructivist way and engages students in an active explorative learning. CCRI approach advocates the use of cooperative learning groups and constructivist ideas to enhance creation of knowledge among pupils during remedial lessons.
Remedial programs designed to assist students in areas where they are having difficulty mastering the required standards at the primary school level have typically been conducted outside the normal school day, which may have resulted in the lack of available research. Many of the programs at the secondary level begin to narrow their focus to one subject. While the focus on individual subjects assists in providing evidence for subject-specific interventions, the research available on Mathematics remedial programs is limited. The few studies available do show that remediation is successful at increasing student achievement in Mathematics (Mross, 2003). Remedial math programs can lead to the success of all students and can assist both schools and students in meeting the expectations of stakeholders (Mross, 2003). However, in order to meet the requirements for research-driven programs, more research is needed on remedial education and its effects on students’ achievement especially in primary schools. It is with this in mind that this study explored the impact of CCRI on pupils’ motivation and achievement in Mathematics.
According to Burris and Garton (2007), the positive impact of constructivist approaches on pupils’ Mathematics dispositions abounds in the education literature. Even though most teachers have heard about the potential of the use of the constructivist instructional strategies to improve pupils’ academic performance (Kim, 2005), there is little research that has examined the use of CCRI strategies in Kenya. Most Teachers usually struggle between their desire to cover a lot of materials as prescribed in the syllabus and the necessity of using more time-consuming methods that allow pupils to construct meaning from their lessons (Franklin, 2001). There seems to be a general haste to cover topics without given pupils the opportunity to acquire deeper understanding of the topics (Anamuah-Mensah, Mereku & Ghartey-Ampiah, 2008).
Problem Statement
The relevance of Mathematics in all careers cannot be overstated. Low proficiency levels in the subject not only affect learners’ and school performance. It also adversely affect society and the economy in general because Mathematics is needed in virtually every career (Robinson et al., 2014). Perennial poor performance in the subject in KCPE Examinations among candidates in Kenya has raised concern among researchers, teachers, parents and other stakeholders. In order to meet the needs of these pupils, many schools are implementing interventions to enhance their achievement in Mathematics. Such interventions are expected to assist those at risk in gaining the necessary skills to meet the required standards on standardized testing. Schools and education specialists need to identify evidence-based interventions that could help this trend in poor performance in the subject. Research suggests that remediation could be an appropriate intervention that can support Mathematics achievement among learners. CCRI approach is designed to give students extra instruction to help them overcome challenges in the areas where they are having difficulties. While some research exists on remedial Mathematics programs, more research is needed. CCRI is one such approach that could be of help in enhancing learners’ achievement in Mathematics. Acknowledgement of gender differences in achievement in the subject is important as well when considering interventions for Mathematics. Previous KCPE Examination results indicate that boys have continued to outshine their female counterparts in their performance in Mathematics over the years. It is therefore important to examine the impact of CCRI on learners’ achievement and motivation by gender to ensure that both male and female students benefit from the intervention.
Purpose of the Study
This study investigated impact of CCRI teaching approach on pupils Achievement in Mathematics.
Specific Objectives of the Study
The specific objectives of the study were to:
Research Hypotheses
The following two hypotheses were tested at an alpha level of 0.05 alpha level of significance:
Theoretical Foundations of Cooperative CCRI
Constructivist model focuses on construction of knowledge in the learners’ mind through active involvement. Proponents believe that every student has different learning experiences. Therefore, a teacher has to be aware that knowledge is constructed differently in the learners’ mind. The pre-existing knowledge that students have is based on their experiences that are constructed in their mind (Taber, 2006).
The teaching and learning strategies informed by constructivism are powerful in creating meaningful learning processes helpful to learner. The meaningful learning process helps students to understand difficult concepts in Mathematics through an active learning process. According to constructivists, learning takes place when individuals participate actively in meaningful activities. Learning is an active process in which a learner is engaged in constructing meaning whether from text, dialogue or physical experiences (Osborne & Wittrock, 2003). Emphasis is laid on students’ development of knowledge through active discussion processes that link new knowledge to prior knowledge. Constructivist theories includes; cognitive constructive theory advanced by David Ausubel, social constructivist theory advanced by Lev Vygotsky and social learning theory advanced by Bandura.
In the constructivists’ model, students actively mediate the input by trying to make sense of it and relating it to what they already know about the topic (Wachanga & Mwangi, 2004). This constructivist process is important because students build their own representation of new learning which would otherwise have been retained as relatively meaningless and inert rote memory (Good & Brophy, 1995). Views of constructivism include the fact that knowledge can never be totally transferred to another person; knowledge is as a result of a person’s interpretation of experiences influenced by factors such as age, gender, race or knowledge base (Ozmen, 2004). In essence some aspects of it are lost during translation when knowledge is transferred. Secondly, individuals make observations, test hypotheses and draw conclusions about events that are consistent with one another. This leads to consensus about different people’s view of the world. Thirdly, it has to do with the formation and changing of knowledge structures, addition to, deletion from and modification of these interpretations. The process of concept formation involves identifying and enumerating the data that are relevant to the problem, grouping those items according to some basis of similarity and developing categories and labels for the groups (Joyce & Weil, 1980).
Although constructivism is a learner-centred theory of teaching, a constructivist teacher works to monitor and direct students learning from a perspective that understands how learning is contingent upon each individual’s existing conceptual structures. Constructivist theory informs the teacher that each learner needs time, space and suitable experiences to support the learning process; but also that minimal guidance during learning is unlikely to lead to desired outcomes (Baker, Rieg, & Clendaniel, 2006).
CCRI is one example of a group task in which students can work together on a given task until all group members have successfully understood and when the task is over the teacher evaluates the academic success of each student (Wachanga & Mwangi, 2004)). The knowledge learned, should enable them to apply in real life situations and show how it affects people in their daily lives. The approach is therefore likely to motivate students by engaging them in a group tasks in which they are expected to realize that they are mutually responsible for one another’s learning as well as their individual academic success.
CCRI is a learner-centered approach that utilizes meaningful interactions to address challenging issues in Mathematics performance. Learning in this sense is an active, self-regulated, constructive, situated and social process (Bransford, Brown & Cocking, 2000). This means that learning is procedural and learner centred. The teacher is required to provide guidance which allows pupils to create their own meaning otherwise it does not guarantee meaningful learning (Novak, 2002).
The conceptual framework used in this study is based on the constructivist theory of learning in which a teacher serves as a facilitator who attempts to structure an environment for effective learning. This makes it possible for the learner to organize meaning at a personal level (Cooper, Jackson, Nye & Lindsay, 2002). The study is also based on the assumption that students’ failures depends on the quality of instruction and not lack of student’s ability to learn (Levine, 1985). The framework is represented diagrammatically in Figure 1.
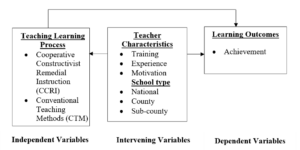
Figure 1: Conceptual Framework for determining the Effects of CCRI on pupils’ Achievement in Mathematics
Figure 1 shows the relationship of variables for determining the effects of using CCRI on primary school pupils’ achievement in Mathematics. Learning outcomes are influenced by various factors. These include: teacher characteristics and classroom environment as shown in the figure. These are the intervening variables which had to be controlled. Teacher training prepares the teacher, determines the teaching approach a teacher uses and how effective the teacher uses the approach (Collier et al., 2004). Learners’ age, gender, entry behaviour and hence their classroom environment determines what they are to be taught. The type of school as a teaching environment affects the learning outcomes. Therefore, only public primary schools were selected for the study. To control for teachers’ characteristics as a source of internal validity, teachers of equivalent training and experience were chosen. It was assumed that teachers of equivalent training and experience teach at the same level. Standard eight pupils who are approximately of the same age were involved in the study to avoid the threat of maturity to internal validity. It was therefore assumed that their age difference did not affect the study.
Research Design
Primary school classes exist as intact groups and school authorities do not allow classes to be dismantled and reconstituted for research purposes (Njoroge, Changeiywo, & Ndirangu, 2014). Since classes exist as intact groups, the study used Solomon’s Four Non-equivalent Control Group Design which is appropriate for quasi-experimental studies. The research design enabled the researcher to determine the cause and effect of the CCRI intervention on learners’ level of achievement in Mathematics. Through this design, the Experimental Groups were exposed to the CCRI treatment for a period of five weeks while the Control Groups were taught using CTM for the same period of time. The design involves random assignment of intact classes to four groups. The design is shown in Figure 2.
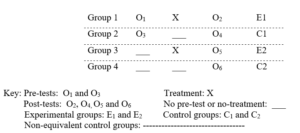
Figure 2: Solomon’s Four Non-Equivalent Control Group Research Design
The selected groups were randomly assigned to Control and Experimental groups. To control for interaction between selection and instrumentation, the researcher ensured that the conditions under which the instruments were administered were kept as similar as possible in all the schools selected (Johnson & Onwuegbuzie, 2004). Also, the effect of maturation was taken care of by the short period that the study took.
Teachers’ gender, training and experience were controlled by choosing teachers of equivalent training, the same gender and teaching experience. Therefore, teachers from the selected schools were male graduates with a minimum of five years teaching experience. According to Borg and Gall (2003), Solomon’s Four Non-equivalent Control Group Design is helpful to the researcher to achieve four main purposes. The design is helpful in assessing the homogeneity of the groups before administration of the treatment and the effect of the experimental treatment relative to control condition. It also enabled the researcher to assess the interaction between pre-test and treatment conditions as well as the effect of the pre-test relative to non-pre-test.
Population of the Study
The study was conducted in four Public Primary Schools drawn from the six wards of Bomet East Sub-County. This sub-county was chosen because performance in Mathematics in KCPE Examinations has been poor over the years in the sub-county compared to other sub-counties within the County. The target population for the study was all class 8 pupils in primary schools within the Sub-County. Preliminary information from the statistics obtained from the Sub-County Education Office indicated that a total of 18,268 pupils from all primary schools in the sub-county registered for 2022 KCPE Examinations. However the accessible population of the study comprised of a total of 6,343 learners in public primary schools within the sub-county. At this level, the pupils are assumed to have developed a stable internal motivation towards Mathematics learning. These conditions were necessary to allow for manipulation of intervention (CCRI) and determine its effects on pupils’ Achievement in the subject.
Sampling Procedures and Sample Size
The unit of sampling was primary schools rather than individual learners because Primary schools operate as intact groups (Borg & Gall, 2003). The sub-county has 400 established co-educational public primary schools with approximately 20,268 KCPE Candidates for the year 2022. Creswell and Creswell (2018), argues that there is no strict rule for obtaining a sample size. However, Fraenkel and Wallen (2000), recommended at least 30 subjects per group.
In the present study, about 211 pupils from four co-educational public primary schools were selected for the study, with each school having approximately fifty students were involved in the study. CCRI was used to teach students in the Experimental Groups while CTM was employed to teach students in the Control Groups. The sampling techniques used in the study for selection of schools and students to participate included purposive sampling, simple random sampling and stratified sampling.
Bomet East Sub-county has five wards. These wards include: Kipreres, Kembu, Longisa, Chemaner and Merigi. This structure enabled the use of stratified sampling in which four schools were selected from each of the four wards were randomly selected guided by the research design. To ensure that the four public primary schools selected are located far apart from each other and to eliminate diffusion of information regarding treatment from the Experimental Groups to the Control Groups, one school was picked from each of the four randomly selected wards out of the five wards of the Sub-county. Table 6 shows the approximate number of respondents per group used in the study.
Table 6: Number of Respondents per Group and Distribution among the four Wards selected
| Group | Type of Group | Respondents (N) | Ward | ||
| Gender | Total | ||||
| Male | Female | ||||
| E1 | Experimental 1 | 32 | 20 | 52 | Kipreres |
| C1 | Control 1 | 20 | 25 | 45 | Kembu |
| E2 | Experimental 2 | 27 | 31 | 58 | Longisa |
| C2 | Control 2 | 24 | 32 | 56 | Chemaner |
| Total | 103 | 108 | 211 | ||
Source: Research Data, 2022
Table 6 shows that the number of respondents selected from the four wards for the study adding up to a cumulative total of 211 pupils. According to the Solomon’s Four Non-equivalent Control Group Design, the four schools selected for use in the study represented the Sub-county as a whole.
A Mathematics Achievement Test (MAT) was used as data collection instrument for both the pre-test and post-test. Items in the MAT were adapted from the KCPE Examination past papers and modified to make them suitable for use in the study. This instrument was used to measure pupils’ proficiency in Mathematics in terms of achievement. The conceptual understanding of the topic covered after the intervention was best measured by asking pupils to show their working as opposed to merely giving answers from the provided multiple choices provided as in the case of KCPE standard exam
The two Experimental groups received CCRI treatment conducted by the Mathematics teachers for a period of five weeks guided by a structured Scheme of Work specifically prepared for the intervention while the Control Groups were taught using conventional methods. During the sessions, students organized into groups of five students each. Pre-tests were administered to the students in the Experimental Group 1 (E1) and Control Group 1 (C1) to measure their level of achievement in Mathematics at the beginning. Post-tests were administered to all the four groups at the end of four-week period. MAT was used to obtain score on pupils’ achievement in Mathematics. The scores obtained were recorded, coded and analyzed in accordance with the two objectives of the study.
A reliable instrument in research should give consistent scores when administered repeatedly (Creswell, 2005). In addition to this the individual scores of the instrument should be meaningful and allow the researcher to draw good conclusions from the sample population being studied (Crewell, 2005). A pilot study was done in neighbouring Narok County to determine the reliability of MAT using KR-21 Formula. According to Fraenkel and Wallen (2000) an alpha value of 0.7 or greater is considered suitable to make possible group inferences that are accurate enough. The instrument was validated by Mathematics experts and its reliability coefficient was found to be 0.82.
The researcher developed an instructional manual and a Scheme of Work (SOW) for teachers involved in the implementation of CCRI. The SOW focused on the objectives, content covered and the teaching and learning activities as prescribed in the KICD Primary Mathematics Syllabus (KIE, 2002). However, the teachers in the control groups were allowed to teach as they have been teaching for the entire four-week period.
Impact of CCRI on Pupils’ Achievement in Mathematics
Pre-test Scores on MAT
T-test analysis of MAT pre-test mean scores for Groups E1 and C1 and for male and female students gave the results in Table 7.
Table 7: Independent Sample t-test of Pre-test Scores on MAT based on Group
| Scale | Group | N | Mean | SD | Df | t-value | p-value |
| MAT | E1 | 52 | 40.30 | 3.82 | 95 | 1.85 | 0.982 |
| C1 | 45 | 38.80 | 4.16 |
ns: non-significant mean differences at p˃0.05 level; MAT Maximum Score = 100
The t-test results in Table 7 shows that the pre-test mean scores were not significantly different, implying that the groups had comparable characteristics and therefore suitable for use in the study.
ANOVA Post-test Scores on MAT based on Groups
After the intervention period all the four groups were post-tested. Post-test mean scores for the four groups are as shown in Table 8.
Table 8: Pupils post-test MAT Mean Scores
| Group | E1 | C1 | E2 | C2 |
| N | 52 | 45 | 58 | 56 |
| Mean Scores | 72.52 | 44.43 | 68.64 | 42.62 |
| Std. Deviation | 6.48 | 5.44 | 5.32 | 6.28 |
MAT Max Score=100
The MAT mean scores were 72.52, 44.43, 68.64 and 42.62 for groups E1, C1, E2 and C2 respectively out of a maximum score of 100. The results in Table 8 indicate that the MAT post-test mean scores of Experimental Groups E1 and E2 (75.52 and 68.64) were much higher than those of the Control Groups C1 and C2 (44.43 and 42.62). This shows that the Experimental Groups performed better than the Control Groups in the MAT. One-way ANOVA was carried out to determine the effect of CCRI on learner’s achievement in Mathematics. Table 9 shows the results of one-way ANOVA on the MAT post-test scores.
Table 9: One-way ANOVA of Post-test MAT Mean Scores
| Sum of Squares | Df | Mean Square | F | p-value | |
| Between Groups | 4835.228 | 3 | 2023.568 | 28.575 | 0.001(s) |
| Within Groups | 9872.503 | 208 | 42.332 | ||
| Total | 14707.731 | 211 |
(s) = significant mean difference at p<0.05 alpha level; MAT Maximum Score = 100
The results in Table 9 indicate that the computed p-value (0.001) was less than the set alpha value of 0.05. Therefore, the differences in MAT mean scores among the four groups were statistically significant at 0.05 alpha level (F (3, 208) = 28.575, p<0.05). Consequently, it was necessary to find out where the difference in achievement existed, a Bonferroni post-hoc analysis was carried out. The results of this analysis are presented in Table 10.
Table 10: Bonferroni Post-hoc Pair-wise Comparisons of the Post-test CAT Mean Scores for the four groups
| (I)Type of Group | (J) Type of Group | Mean Difference (I-J) | Std. Error | Sig. |
| E1 | C1 | 7.5422(*) | 1.1233 | .000 |
| E2 | .4324 | 1.0882 | 1.000 | |
| C2 | 7.4234(*) | 1.0932 | .000 | |
| C1 | E1 | -7.5422(*) | 1.1345 | .000 |
| E2 | -7.5656(*) | 1.0522 | .000 | |
| C2 | 0.5782 | 1.0788 | 1.000 | |
| E2 | E1 | -0.4324 | 1.1232 | 1.000 |
| C1 | 7.5656(*) | 1.0782 | .000 | |
| C2 | 6.8122(*) | 1.0924 | .000 | |
| C2 | E1 | -7.4234(*) | 1.1288 | .000 |
| C1 | -0.5782 | 1.1245 | 1.000 | |
| E2 | -6.8122(*) | 1.5480 | .000 |
The Mean difference is significant at the 0.05 alpha level
Bonferroni post-hoc pair-wise comparisons of significance for a difference between any two means results in Table 10 shows that there was a statistically significant difference between the pairs of MAT post-test means for groups E1 and C1, groups E1 and C2, groups C1 and E2 and groups E2 and C2 at 0.05 alpha level. However, there was no statistically significant difference in the means between Groups E1 and E2 and Groups C1 and C2. Consequently, H01 was rejected
It was possible to determine the mean gain for the two groups that were pre-tested and later post-tested. The results in Table 11 shows the mean gain between students’ MAT pre-test scores and post-test scores.
Table 11: Comparison of Students’ Mean Scores with their Mean Gain in the CAT
| Group | E1 (N=52) | C1 (N=45) | Overall (N=97) |
| Post-test Mean Scores | 72.52 | 44.43 | 58.475 |
| Pre-test Mean Scores | 40.30 | 38.80 | 39.550 |
| Mean Gain | 32.22 | 5.63 | 18.925 |
MAT Maximum Score = 100
The results in Table 11 indicate that both Groups E1 and C1 gained from the teaching. However, the E1 group taught through CCRI had a higher mean gain than the C1 group implying that the CCRI approach resulted in higher achievement than the CTM. Therefore, CCRI enhanced the achievement of students who were in the experimental groups more than those in control groups which were taught through CTM. This implies that CCRI enhanced students’ achievement in Mathematics more than the CTM.
Impact of CCRI on Pupils’ Achievement in Mathematics based on gender
Pre-test Scores on MAT based on Gender
Table 12: Independent Sample t-test of Pre-test Scores on MAT based on Gender
| Scale | Gender | N | Mean | SD | Df | t-value | p-value |
| MAT | Male | 52 | 49.2 | 3.82 | 95 | 1.72 | 0.855(ns) |
| Female | 45 | 46.9 | 4.16 |
ns: non-significant mean differences at p˃0.05 level; MAT Maximum Score = 100
The post-test shows that the MAT mean scores for female students is almost equal to that of male student being a mean of 86.53 while that of the female students was 84.39 out of a total mark of 100. This therefore shows CCRI improved the achievement in Mathematics equally for both boys and girls. Table 13 shows the results of t-test on MAT mean scores for both male and female students exposed to CCRI: M=103; F=108.
Table 13: Independent Sample t-test on Post-test Scores based on Gender on MAT
| Levene’s Test For Equality of Variances | t-test for Equality of Means | |||||
| F | Sig. | T | Df | p-value | ||
| MAT | Equal variances assumed | 1.185 | .192 | .338 | 119 | .528(ns) |
| Equal variances not assumed | .339 | 208.255 | .608 | |||
ns: non-significant mean differences at p˃0.05 level; MAT Maximum Score = 100
The results in Table 13 shows that there was no significant gender difference in achievement in Mathematics at the end of CCRI intervention (t(119)= 0.338, p˃0.05). Therefore, Hypothesis 2 was accepted. Table 14 shows the mean gain for boys and girls on skills acquisition.
Table 14: Students’ Mean Gain in MAT based on Gender
| Group | Male (N=52) | Female (N=45) | Overall (N=97) |
| Post-test Mean Scores | 72.52 | 68.43 | 70.475 |
| Pre-test Mean Scores | 41.45 | 36.72 | 39.085 |
| Mean Gain | 31.07 | 31.71 | 31.39 |
MAT Maximum Score = 100
The results in Table 14 show that the mean gains for male and female students were 31.92 and 31.71 respectively. Thus, both boys and girls equally benefited from the CCRI approach in terms of achievement in Mathematics.
The determination of the effect of gender on students’ achievement when CCRI Teaching Strategy is used to teach Mathematics was guided by Hypothesis 1. The MAT post-test mean scores for both male and female students was found to be almost equal with that of male students being 72.52 while that of the female students was 68.43 out of a maximum of 100. A comparison of this MAT post-test scores with pre-test scores shows that the mean gain for boys was 31.07 while that of girls was 31.71. This therefore shows that CCRI improved the achievement of both boys and girls.
The post-test MAT t-test results show that there was no significant gender difference in achievement among boys and girls exposed to CCRI. This therefore implies that both boys and girls improved in achievement at the end of CCRI intervention. Hypothesis two was therefore accepted. Siegle and Reis, (2007) points out that achievement in Mathematics is the basis for full promotion and improvement of the status of women for self-reliance. Interactive methods of teaching such as CCRI have been found to rank among the factors that enhance meaningful learning in Mathematics classes. None method of teaching has emerged the best in teaching Mathematics content for understanding. However, Mathematics teachers who integrate a number of teaching approaches and match the content they are teaching with an appropriate method have succeeded in effective and meaningful learning of Mathematics.
Instructional methods employed in teaching should be as participatory in nature as possible and endeavour to teach large classes of learners “how to learn”. The use of teaching aids and facilities in order to improve Mathematics teaching has greatly increased in recent years (Đurđanović, 2015). The reason is that, Mathematics materials and construction instruments arouse great interest among the learners, encourage cooperation and interaction among learners in group work, enhance stimulus variation and consequently motivate them to learn. CCRI is a good example of such approaches which encourage both boys and girls to effectively acquire skills in Mathematics which have direct application in our day to day life. This eventually contributes to meaningful learning of Mathematics.
Summary of the Major Findings of the Study
The following are the major findings of the study:
The CCRI approach enhances students’ achievement in Mathematics more than the CTM. It was also observed that gender does not affect students’ achievement in Mathematics when they are taught through CCRI approach.
Mathematics should be taught using methods that will help learners to get concept of logic and reasoning thus enhancing their achievement. Effective classroom practices and curriculum materials should not only focus on cognitive factors but also on non-cognitive factors such as Mathematics anxiety. Such anxiety could be overcome by using innovative T/L methods which encourage learner participation through problem solving techniques. Teachers have to implement techniques that have been found to reduce such anxiety which is rampant among students. On the other hand, students have to use the findings of the study to improve understanding about their own math anxiety. They can reflect on how their own math anxiety fits in with the findings of the study and they may try to know the cause of their own math anxiety and use the strategies.
Students taught through CCRI approach performed better in the MAT than those taught through CTM irrespective of gender implying that CCRI would be suitable for teaching both boys and girls. Therefore, education authorities in Kenya should encourage Mathematics teachers to use this method and teacher education institutions could also make it part of their teacher training curriculum content.